ERNEST MOYER'S RESEARCH
of the
Four Great Egyptian Pyramids
Copyright Ernest P. Moyer, author
March, 2001
Introductory
All four great pyramids have entrance passages on their north faces. In addition, the Bent has a second entrance on the west side high up on the structure,replica orologi italia while Giza 2 has a second entrance cut into bedrock outside the base. The passages are very small; they are roughly one meter square. They cannot be negotiated except by crouching on hands and knees. The small entrances are in sharp contrast to the huge size of the Pyramids.
(Please note that I do not examine other passage properties in this paper. Here I concentrate on the slopes only.)
Except for the bent pyramid west passage all slope downward linearly from the entrance until they reach the level on which they terminate, leading to or at a chamber near the center of the respective pyramids. The entrance on the beste replica uhren west face of the bent pyramid changes angle of decline part way down.
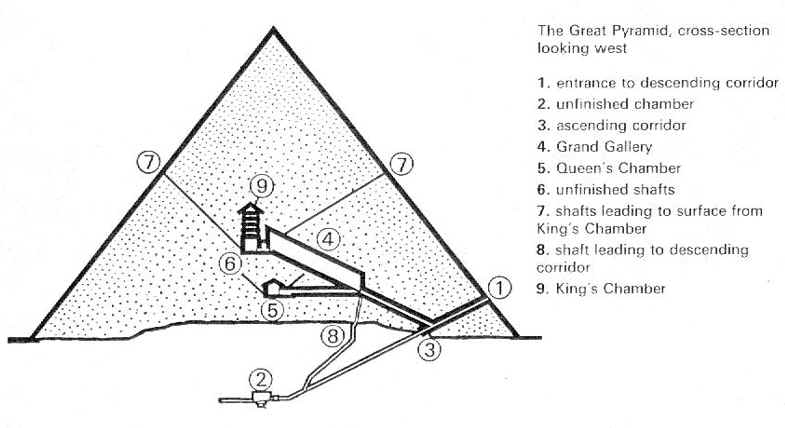
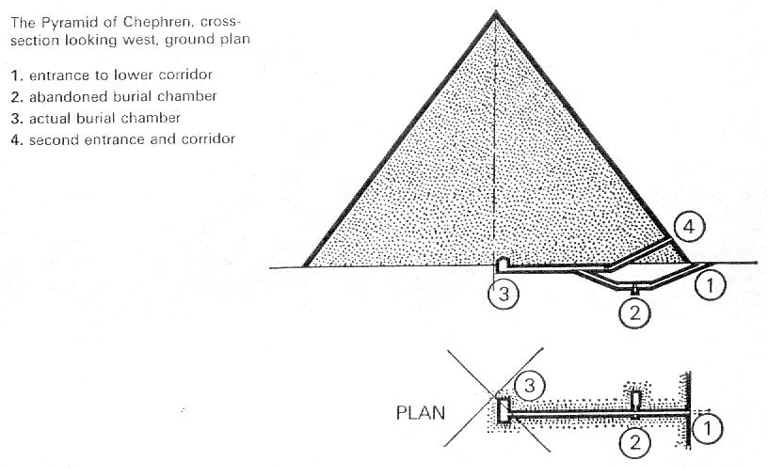
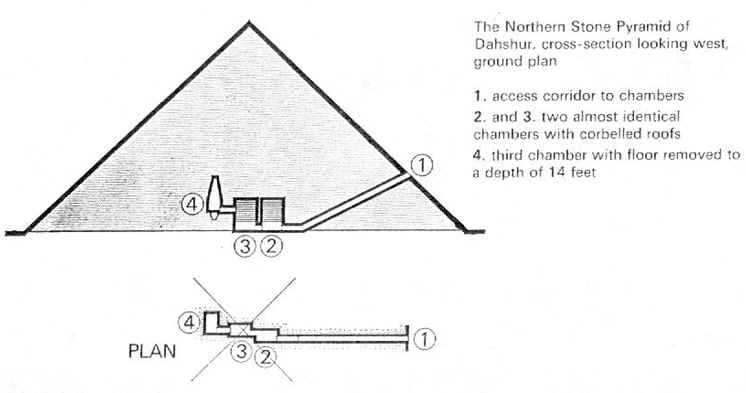
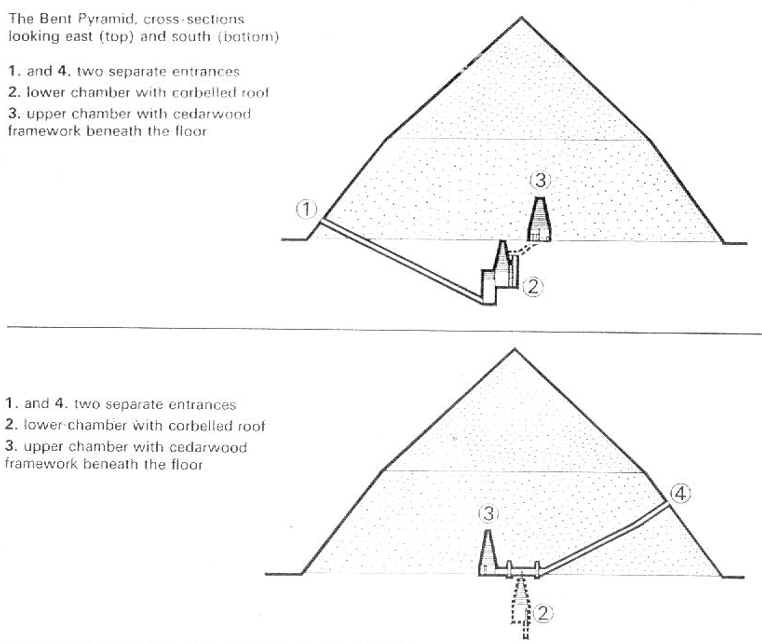
Refer to the cross section diagrams of
the respective pyramids. These diagrams are from the book by I. E. S. Edwards,
The Pyramids of Egypt, The Viking Press, New York, 1972. This edition
is a reprint in full color of the 1961 edition by Penguin Books. Please note
that I do not make the King assignments shown by Edwards.
 |
 |
 |
 |
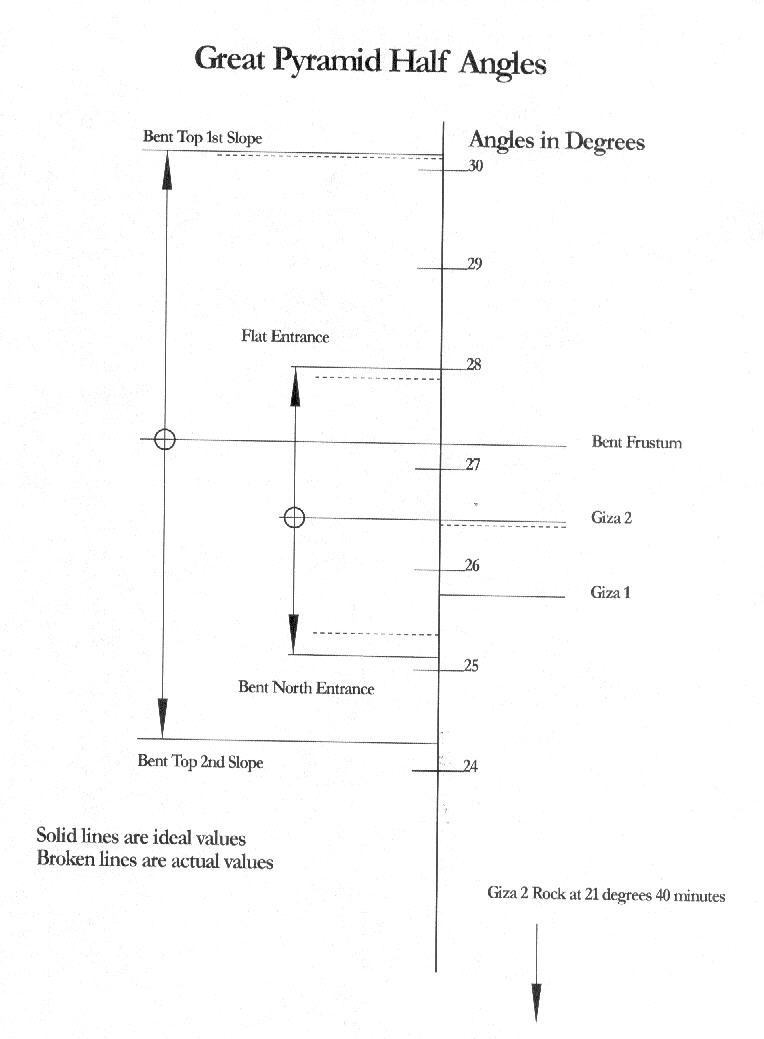
The angles of the slopes vary from 24° to 30°. The angle of the passage cut into bedrock below the base of Giza 2 slopes at 2l° 40'.
This table summarizes the angles of the passage slopes of the several entrances.
My sources are the same as shown in the
preceding paper.
| Pyramid | Entrance Passage Angle |
| Giza 1 North | 26° 31' |
| Giza 2 North | 25° 55' |
| Bent West 1 | 30° 09' |
| Bent West 2 | 24° 17' |
| Bent North | 25° 24' |
| Flat North | 27° 56' |
| Giza 2 Bed Rock | 21° 40' |
No satisfactory explanation for the various slopes has ever been offered. Over the many centuries a mythology developed that the passages point to the north star. This idea is incorrect for two reasons. First, the angles are off as much as six degrees from the true north polar position on the celestial sphere. The angle necessary to point at the north polar position is the same as the latitude at which the pyramids are located, 30°. Only the one bent passage is near this angle, and it is on the west face.
Second, the north star is not fixed with time. Due to the precess of the replica sunglasses equinoxes, the stars drift past and around the north polar position at a rate of about one degree in seventy years. This means that any star which may have been in the north pole position in 2700 BC has long since drifted to another location, and that Polaris, the present pole star, will drift away also, if the earth continues in its present motion. Since 2700 BC, the earth has moved around the great circle almost 70 degrees. This covers a considerable area of the northern sky because the earth is tilted at an angle of 23° to the plane of its orbit.
For these reasons it appears that the builders of the great pyramids did not intend the entrances to point to any star. However, location on the north faces of the pyramids pointing near the north polar position draws attention to them.
Examination of the passages shows that they were designed as part of the geometric properties of the pyramids.
The Giza Entrance Passage Slopes
Giza 1 has a measured entrance passage angle of 26° 31'. This angle is very nearly the half-angle of the 3-4-5 design slope of Giza 2 of 53° 3'. The ideal half-angle of the 3-4-5 is 26° 34'; the error from the ideal is 3'.
Within measurement error:
The angle of the Giza 1 entrance passage slope is exactly one-half the angle of the exterior slope of Giza 2.
Furthermore, the measured entrance passage angle of Giza 2 is 25° 55'; the ideal half-angle of the Giza 1 exterior slope is 25° 55'. Therefore:
Giza 2 has an entrance passage whose angle is exactly one-half the angle of the exterior face slope of Giza I.
The two pyramids complement one another in their exterior face angles and their aaaaa replica watches entrance passage angles.
This fact is surprising and has never been discussed in any of the literature on the pyramids. No student of the pyramids has ever reported this fact, as far as I am aware.
But this fact has a dramatic implication:
The two great Giza pyramids were designed as one project.
Both designs had to be known before either was built.
They could not have been designed and built independently of one another.
The Daschur Entrance Passage Slopes
If the four pyramids are tied together by exterior dimensions, and the two Giza structures are tied to one another by their entrance passages, do the entrance passages of the Bent and the Flat also demonstrate mathematical connection with one another, or with the two Giza pyramids?
The entrance on the west side of the Bent begins at an angle of 30° 09'; part way down it changes to 24° 17'. These cannot be half angles of any exterior, since double of the first is 60° 18', and double the second is 48° 34'. The last is about three degrees less than the Giza I exterior slope and five degrees higher than the Flat exterior slope. Both are well beyond the error range of any great pyramid measured face slope.
The solution to the query is not far away. The sum of the angles of the two passage slopes at 54°26' is the same as the slope of the exterior of the Bent frustum, within 2' of angle.
The sum of the two angles of the Bent west passage slopes is the same as the exterior angle of the Bent frustum at 7/5.
In this case the sum of the Bent pyramid west passage angles appear to reflect the pyramid frustum exterior slope.
But what of the entrance on the north face of the Bent? It has a measured angle of 25° 24'. Double this angle is 50° 48', at least one degree less than the exterior slope of Giza I, and beyond the error range we have encountered thus far.
Also, the entrance of the Flat pyramid slopes at 27° 56'. Double this is 55° 52'. This last value is about 1° 24' greater than the slope of the Bent frustum, and again well above the error range we have encountered.
Significantly, the sum of the north passage angles on both the Flat and the Bent is 25° 24' + 27° 56' = 53° 20'. This is about 12' greater than the ideal exterior slope of Giza 2, somewhat above the usual error range, but a plausible relationship. (12' on 53° is 12 parts out of 3200, or an angular error less than 0.4%.) Within measurement error:
The sum of the angles of the two north entrances passages at Daschur is equal to the angle of the exterior slope of Giza 2.
This demonstrates another profound implication. If the sequence of construction saw the Daschur pyramids built prior to the Giza pyramids:
The Giza 2 Bedrock Passage
But what of the entrance cut into bedrock outside the base of Giza 2, the only passage we have thus far not considered. It has an angle of 21° 40'. Double this is 43° 20'. The value is 4' greater than the slope of the Bent top, and about 16' less than the exterior slope of the Flat. Thus it appears that
The angle of the slope of the Giza 2 outside passage is the half-angle of the exterior slope of the Bent top.
Until now no one could propose a satisfactory reason for this Aextra@ passage dug into the bedrock outside Giza 2. Now we can understand. The regular entrance slope reflected Giza1; it could not serve to reflect the Daschur structures. Therefore,
The outside Giza 2 passage was an extra cut to show a relationship to the Daschur Bent pyramid.
From this fact we see that the bedrock passage of Giza 2 reflects a structure at Dashur. The sum of the passage angle slopes of the two Dashur north passages reflect the same structure at Giza.
Hence, Giza 2 serves as the focal point to tie the Giza structures to the Daschur structures, based strictly on their passage slope angles.
The four structures are tied to one another according to the angles of the slopes of the exteriors and the angles of the slopes of the entrance passages, where the latter represent the half angles of the former.
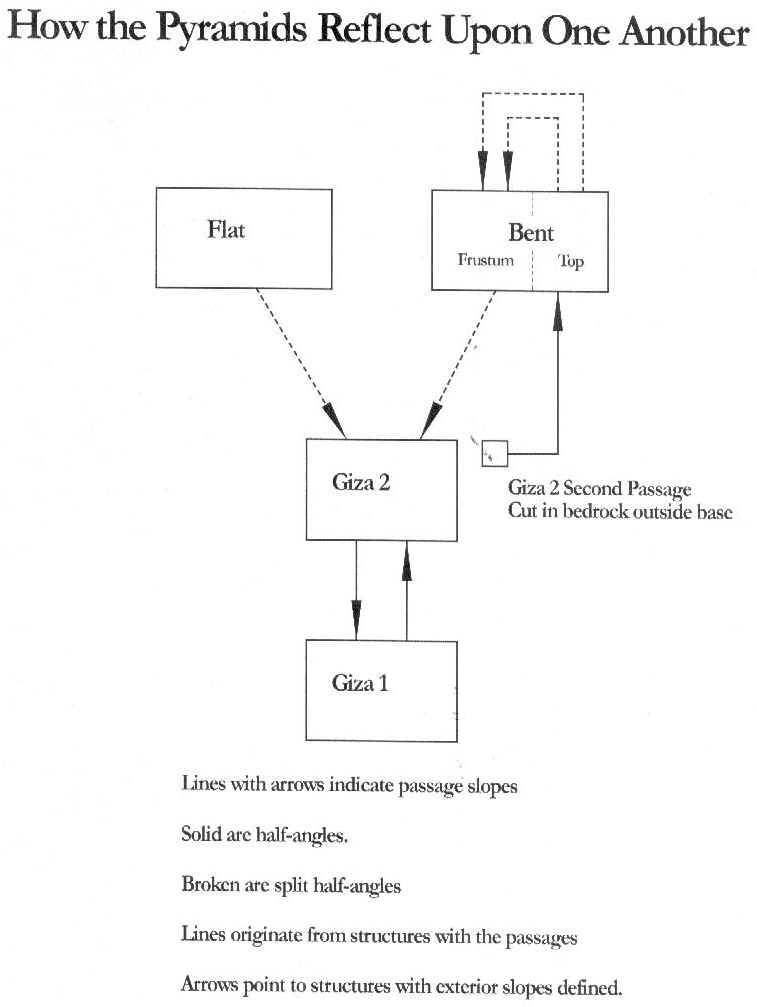
I represent the relationships in the
Figure. The solid lines show an exact half angle. The tail of the arrow
originates on the block representing the pyramid containing the passage; the
head of the arrow points to the pyramid that it represents in half-angle. The
dashed lines represent those passages that sum to an exterior slope, but are
not exact half angles.
 |
The Reason for the Split Half Angles
Note that the entrance passage slopes at Giza directly represent half-angles of one another and of the Daschur Bent top slope. Stated otherwise:
The angles of the passage slopes at Giza are directly one-half the angles of the respective exterior slopes.
In contrast the angles of the entrance passage slopes at Daschur are not directly the half angles of exterior slopes but sum to exterior slope angles. The angles of the Bent west passage sum to the Bent top angle, while the angles of the Daschur north passages sum to the exterior angle of Giza 2.
The angles of the passage slopes at Daschur are split half angles which sum to the angles of the respective exterior slopes.
Why did the builders give slopes in the structures at Daschur that are not directly half-angles? Why did they make them add to a sum that represents the angles of the respective exterior slopes?
I found the answer by accident. I was using my engineering slide rule to compute the tangents of the several angles, and to determine the departure of the Daschur entrance passage angles from the ideal half angles. The difference between the two angles on the Bent west side is 5° 52' (30° 09' - 24° 17'). One half of this angle is 2° 56'. I set the cursor on my slide rule to find the tangent of 27° 14', the Bent frustum half angle. (I was looking for the ideal half-angle of the frustum slope.) This gave me a tangent reading of 0.515. I then looked for the tangent reading of 2° 56', half of the difference of the two angles.
To my surprise I did not need to move the cursor on the slide rule. (The slide rule is laid out with different scales that are multiples of ten to one another.) The value of the tangent of 2° 57' is 0.0515, one-tenth of the tangent of the frustum half angle.
In other words, the tangent of the difference between the two slope angles divided by two is one-tenth of the tangent of the average of the two slope angles.
This may be stated in mathematical expression as:
tan ([A - B]/2) = K tan ([A + B]/2)
where A and B represent the two angles.
This is a trigonometric formula, familiar to modern mathematics. It was not known in the historic mathematical repertoire of the ancients.
In this case (A + B) is the exterior slope angle, and K = 0.1.
Tabulating different split angles and K
values shows how the angles vary. I offer this in order for the reader to
grasp the practical constraints that faced the designer.
| K | ||||||
| 0.05 | 0.1 | 0.2 | 0.5 | |||
| (A + B) | 2 (A + B) | tan | Split Angle (A - B) | |||
| 20° | 10° | 0.1763 | 1.01° | 2.02° | 4.04° | 10.07° |
| 30° | 15° | 0.2679 | 1.53° | 3.07° | 6.13° | 15.26° |
| 40° | 20° | 0.3640 | 2.09° | 4.17° | 8.33° | 20.67° |
| 50° | 25° | 0.4663 | 2.67° | 5.34° | 10.65° | 26.25° |
| 53° 20' | 26° 40' | 0.5022 | 2.88° | 5.75° | 11.47° | 28.19° |
| 54° 26' | 27° 13' | 0.5142 | 2.95° | 5.89° | 11.74° | 28.84° |
| 60° | 30° | 0.5774 | 3.29° | 6.61° | 13.17° | 32.21° |
The designer had to choose angles that would be realistic. He would not choose a K value of 0.5 because the split angles become too great. We can see that even for a K value of 0.2 the split angles of 11° at the design slopes of the pyramids is too great. This would require passage slopes on the order of 30° and 20°. These values would interfere with our recognition of the simple half angles. Therefore, he went to lower K values.
He chose a simple K value of 0.1 because it would become apparent to someone attempting to investigate the reasons for the slopes. This is exactly what I did. If he had chosen a K value of some unusual number, such as 0.18, the value would not have been obvious. I get the uncanny feeling that he knew I would be using a slide rule with multiple decimal scales. Or, stated more realistically, he knew that the discovery of his design would depend upon someone familiar with such mathematical methods.
Then, in order to separate the 53° 20' of the Giza 2 exterior slope from the 54° 26' of the Bent top slope he used 0.1 K value for the first, and 0.2 K value for the second. This gave him 5.75° and 2.95°. If he had used 0.1 K value for both they would have been too close to one another. Thus he was constrained by what was practical, and how a future investigator would discern his design intent.
These facts raise a very profound concept.
The designer recognized that his knowledge would be lost, and that a time might come when it would be rediscovered. The vast teams of workers who built the pyramids certainly did not know. Nor does it seem reasonable that the kings who financed them knew of these designs. Otherwise knowledge of the specific details of the design should have come down to us. The designs had no meaning unless someone could rediscover them. History has demonstrated this fact. How much have the generations struggled to understand the pyramid designs, but with a large burden of mythology still attendant upon the pyramid phenomena, even to this day?
We can see that the designer had to have a table similar to the above in front of him when he made his design choices, or some other mathematical computational method which would permit him to size up his choices.
I now had the answer to the pyramid entrance passages. But I was able to obtain it only because I was not burdened with mythological foolishness.
I shall now review the steps in the computation to make this more clear.
The designer took the half angle of the Bent frustum, 27°14'. He then took one-tenth of this angle to compute a new incremental angle. (0.1 X tan 27° 14' = 0.0515 = arc tan 2° 57'). He then added this to the half angle to obtain 27° 14' + 2° 57 = 30° 11'. The measured value of the passage first slope is 30° 09', or only 2' less than the ideal model.
He then took the incremental value and subtracted it from the half-angle to obtain 27° 14' - 2° 57' = 24° 17' ideal. The measured angle of the second slope of the Bent west passage is 24° 17', or exactly the computed ideal.
From this procedure we can see that:
The designer had to understand the principles of trigonometric mathematics, with its definition of tangents, in order to perform his designs.
This procedure, when applied to the Bent and Flat north passages, shows the place of the 12' error in the measured slope.
The tangent of one-half of the Giza 2 exterior of 53° 08' is 0.500. (Note that this is a 3-4-5 triangle.) One-twentieth of this is 0.025. The angle whose tangent is 0.025 is 1° 26'. If this is added to the half angle of 26° 34' we obtain 28° 0'. The slope of the Flat entrance is 27° 56', or 4' less than the computed ideal value.
When we subtract 1° 26' from 26° 34' we obtain 25° 8'. This is 16' below the measured value for the Bent north entrance passage angle.
The error appears in the Bent north passage. This may be due to error in the measure of the slope, the construction, or, more likely, settling of the structure. As I stated in the previous paper, the Bent has suffered settling sometime in the past. This is evident on both the north and west passages where glaring fractures can be seen. The genius of the construction can be discerned when we note that the Best west passage has suffered almost no significant alteration to the angles, but settling has caused the north passage to increase in slope about 24 cubits from the entrance to a reported angle of 28° 38' . Perring reported a shift in passage angle to 26+°. Edwards reported 25° 24'. This is where the large discrepancy exists.
The designer could have obtained some idea of the practical nature of his goal by drawing a circle diagram, inserting the angle from the center of the circle, and then drawing a line to the opposite intersection of the diameter chord on the circle. This is the famous half-angle theorem propounded by Euclid, some 2500 years later. Euclid was part of the beginning of the march back from a regime of gross ignorance that had prevailed all those centuries. But the pyramid designer did not depend upon simple geometric sketches. The angles were computed, measured, and constructed with exquisite precision.
Several observations may be helpful.
First, the designs are based upon angles, not upon slopes. As shown in the equation above, the designer had to be familiar with angular measurement, increments of arc, and not merely the measure of slopes.
Second, there is an efficacy in design that led me on to the determination of the details. My first step was notice of the half-angles of the two Giza structures. This then caused me to investigate all passage slopes, and angles. We could quickly recognize that the Abent@ passage is in the Bent pyramid, and cause us further to wonder about its application. This led further to calculation of the half-angles in the Daschur pyramids, and the discovery of the sum and differences in the angles.
I felt as though I were being led down a path of mental observation, analysis, and discovery.
This is further testimony to the genius of the designer. He was brilliant in his conceptual execution.
Third, there is a refinement in construction that has withstood nearly 50 centuries. The refinement of measurement by modern observers is also a testimony to his genius in that he was able to build to exacting tolerances that could not be discerned until modern measurement techniques. The average error from the computed to the measured values is less than 0.4' of arc, even if we include the Bent fractured passage. Ignoring that passage, the average error is less than 0.2' or arc. This fact is incredible. Most modern structures do not pretend to two parts out of 5400 of arc, or about 0.036%. The equivalent angular displacement is two feet in one mile.
Fourth, we are left with a strong
suspicion that the designer knew something about incremental mathematics, what
today we term differential calculus.
 |