ERNEST MOYER'S RESEARCH
Exterior Design
of the
Four Great Egyptian Pyramids
Copyright Ernest P. Moyer, Author
March, 2001
Introductory
The Great Pyramid at Giza (Giza 1) is a gem in pyramid building, and receives virtually all of the attention. But it was not built in isolation. It was part of a construction project that included three other large pyramids. One of those is the Giza companion (Giza 2). The other two are located at Daschur, usually denominated the Flat and the Bent. Together, those four constitute more than 70% of the total Egyptian pyramid volume.
The step pyramid at Saqqara, and the Meidum pyramid appear to be evolutionary projects approaching the size of the large four, but all other pyramids are puny in comparison.
Examination of the size and the slope of the exteriors of the four great pyramids show them related to one another mathematically.
I shall review the technical data of each in turn, in the sequence of the Bent, the Flat, and Giza 2, while reserving most attention for Giza 1. I shall then show how they are related.
My sources are:
1. W. M. Flinders Petrie, The Pyramids and Temples of Gizeh, Field and Tuer, London, 1883, First Edition.
2. J. H. Cole, Determination of the Exact Size and Orientation of the Great Pyramid of Egypt, Survey of Egypt, Paper #39, Government Press, Cairo, 1925.
3. H. Vyse and J. S. Perring, Operations Carried out at the Pyramids of Egypt in 1837, 3 vols, J. Fraser, London, 1840-1842.
4. A. Fakhry, The Monuments of Sneferu at Dashur, in two Volumes, Cairo, 1959-1961.
5. V. Maragioglio and C. Rinaldi, L'Architettura delle Piramidi Menfite, in seven volumes, Rapallo, 1964.
Maragioglio and Rinaldi summarized the data collected by most other previous workers. Some of this data was reported from sources not cited above. Also, their work was not always the most accurate. So we must be careful in accepting their data. Hereafter I refer to this work only as Maragioglio.
The Pyramids at Daschur
The North pyramid at Daschur is the Flat; the South pyramid is the Bent. They are a companion pair, the same as the companion pair at Giza.
North Pyramid at Daschur
Maragioglio twice reported Perring but differently in the two reports.
Maragioglio reporting Perring (#1)
Base 219.42 m (418.74 cubits)
Height 104.49 m (199.41 cubits)
Slope 43o 36' 11"
Maragioglio reporting Perring (#2)
Base Length 219.28 m (418.47 cubits)
Height 104.42 m (199.27 cubits)
Slope 43o 36' 11'
Maragioglio reporting Reisner
Base 218.5 m (416.98 cubits)
Height 104.4 m (199.23 cubits)
Slope 43o 31' 11"
The slope of a 20-21-29 integral Pythagorean triangle is 43o 36' 10".
The Flat pyramid at Daschur was designed as a 20-21-29 integral Pythagorean triangle.
The height of the pyramid was intended to be 200 cubits.
The base length then was determined.
Ideally, the base would be 2 X 209.81 = 419.63 cubits.
This compares to the measured values of 418.74 and 416.98 cubits.
South Pyramid at Daschur
This pyramid is composed of a frustum, topped by a true pyramid shape.
Maragioglio reporting Petrie
Base 188.6 m (359.92 cubits)
Bottom slope 54o 31' 13"
Upper slope 43o 21'
Height from base to bend 49.07 m (93.64 cubits)
Height from bend to top 56.00 m (106.87 cubits)
Total height (200.51 cubits)
Unfortunately, we do not have comparison measurements from other investigators.
Maragioglio personally observed great cracking of the stones comprising the structure. There was settling, not due so much to earthquakes, but to compression of the ground. Therefore, the observed dimensions and slopes may not exactly reflect the original construction.
Given these precautions we can draw some conclusions.
The height of the Bent was designed the same as the Flat at 200 cubits.
The base measurement suggests it was designed at 360 cubits.
In order to show the design parameters I
sketched an outline of the pyramid, compared against the Flat. The figure
shows the design ratios of the various segments.
If the pyramid was designed at 360 base, it was shortened from the base of the Flat by 119.63 cubits.
To help analysis I divided one half of the base of the Flat pyramid into 63 parts. This made each part slightly short of 3 1/3 cubits.
Assuming 3 1/3 cubits, the Bent half-base length would be 54 X 3 1/3 = 179.84 cubits. The full length would be 359.68, or short of 360 by .32 cubits, equal to 6.6 inches.
Or, doing it the other way, assuming that the Bent base is the criteria for dividing the length into integral portions of 3 1/3 cubits, the length of the Flat base would be 60 cubits longer than the Bent, or 420 cubits. This differs from the ideal of 419.63 by 0.39 cubits, or eight inches.
If the Flat one-half base were divided 63 parts for analysis, and maintaining the ratio of 20/21, the height would be divided into 60 parts. This would again give 3 1/3 cubits per part.
From this analysis the height of the bent section would be (28/60 X 200) = 93 1/3 cubits. The measured value is 93.64. The difference is 0.3 cubits from the assumed design ideal.
The height of the top portion would be (32/60 X 200) = 106 2/3 cubits. The measured value is 106.87 cubits. The difference is 0.27 cubits.
These two errors add to 0.57 cubits.
Clearly, the ravages of time and the errors of measurement prevent us from determining more precisely how the designers proceeded with their construction.
This line of analysis leads us to believe that the slope of the frustum was 7/5, or an angle of 54o 28'. This compares with a measured value of 54o 31'.
The slope of the pyramid top would then be 0.94 for an angle of 43o 15'. This compares to 43o 21' measured. (0.94 is equal to a slope of 16/17)
We can see from the diagram that the bent portion protrudes slightly above the slope of the Flat pyramid, if we assume these design criteria. The calculated amount is about 1.6 cubits, 33 inches, or about one yard.
Ideally, we would desire the bend of the Bent pyramid to fall directly on that slope line. The interested reader can perform the calculations to determine how much the base and height values should change to achieve that result.
The Bent pyramid outline apparently was intended to fall within the outline of the Flat,
while constricted by the suggested design criteria.
These design criteria would imply that the pyramid builders used simple arithmetic ratios to achieve their measures.
Giza 2
From Petrie=s measurement:
North side = 8471.9 inches = 410.66 cubits
East side = 8475.2 inches = 410.82 cubits
South side = 8476.9 inches = 410.90 cubits
West side = 8475.5 inches = 410.83 cubits
Calculated mean of the four = 410.80 cubits
Slope = 53o 10' +/- 4' as Athe best statement.@
The crude state of the exterior prevented more precise measurements.
Petrie calculated the height at 5,664 +/- 13 inches = 274.55 +/- 0/63 cubits, for an ideal of 275 cubits.
The ideal slope of a 3-4-5 Pythagorean triangle is 53o 3'.
Giza 2 appears to be designed as as 3-4-5 integral Pythagorean triangle.
Note that the base length of Giza 2 of 410.80 cubits is less than the Flat base length of 419.63 cubits by about nine cubits. I shall return to further discussion.
Giza 1
From Petrie=s measurements:
North side = 9069.4 inches = 439.62 cubits
East side = 9067.7 inches = 439.54 cubits
South side = 9069.5 inches = 439.63 cubits
West side = 9068.6 inches = 439. 58 cubits
Measured slope = 51o 50' 40" (This was a weighted mean up the north face.)
Petrie noted that Athe South face should not be included with the North, in taking the mean, as we have no guarantee that the Pyramid was equiangular, and vertical in its axis.@
Petrie gives calculated height at 5,776 +/- 6 inches. This would be 279.98 +/- 0.29 cubits, for an ideal of 280 cubits.
From Coles measurements:
North side = 230.253 meters = 439.41 cubits
East side = 230.341 meters = 439.58 cubits
South side = 230.454 meters = 439.80 cubits
West side = 230.357 meters = 439.61 cubits
Thus we can see that Cole differed from Petrie on the average around the four sides by no more than +0.03 cubits. Their differences overall appear to be no more than error of measurement.
The difficulty in determining the design criteria for the Great Pyramid is its proximity to three different solutions.
#1: The height of the pyramid represents the radius of a circle, while the base perimeter represents the circumference of the same circle.
It is expressed mathematically as
h = 2 Pi X 4s
#2: The square of the height is equal to the face area of one side.
This is the famous Golden Ratio, or Golden Section, also known as the Divine Ratio.
This ratio was used as a design guide in many ancient structures, has been discussed extensively in mathematical and architectural literature, and is well known in the field of art.
It is expressed mathematically as
a/b = b/(a + b)
The ratio is mathematically unique. Numerical solutions from the above equation are 0.618034 and
-.618034.
I shall return to further discussion of this unique ratio.
#3: The area of a circle is to the square of its diameter as 11 to 14.
This ratio was given by Archimedes (c. 287-212 BC) in his treatise, Measurements of a Circle, Proposition 2.
This is the famous Pi approximation of 3 1/7 = 22/7.
We can now calculate the pyramid dimensions subject to these three different criteria.
From #1:
If the radius of the hypothetical circle is the height at 280 cubits, then the circumference is 2 Pi X h = 1,759.3 cubits. The sum of the Petrie values is 1758.37.
Certainly this hypothesis is correct, within measurement error. The difference is only 0.93 cubits.
From #2:
Solutions based on the Golden Ratio are found as follows:
Let the ratio of one-half the base length, x, to the height, y, be equal to the ratio of the height, y, to the apothem, a.
x / y = y / a
But from the Pythagorean theorem we know that a2 = (x2 + y2).
In order to make this tractable we must square both sides.
x2 / y2 = y2 / (x2 + y2)
This equation is the same form as the Golden Ratio, except that it is expressed in terms of the squares of the elements.
Thus we find that mathematically x2 / y2 = 0.618034.
We obtain 0.616 from the ratio of the measured values of 219.82 / 2802.
The slope of the ideal Golden Ratio is x / y, or the inverse of the square root of 0.618034 = 0.78615. The inverse is 1.2720.
The slope from the measured values is 280/219.8 = 1.274.
Hence we could now conclude that the Great Pyramid was designed around the Golden Ratio.
From #3:
The slope of 11/14 is 0.7857. The inverse is 1.2727.
Compare this with the measured values, and also with the slope determined from the Golden Ratio.
Hence we could conclude that the simple Archimedes ratio of 11/14 was the criteria for the construction of the Great Pyramid.
This would agree with our earlier assessment that the builders used simple arithmetic ratios for their design.
The uncanny part of these criteria is that the values of three important hypotheses all fall within the construction tolerances of the pyramid.
Someone certainly knew his mathematics.
The ideal angles for these three are as follows:
#1 51o 51.2'
#2 51o 49.6'
#3 51o 50.6'
Petrie gave 51o 50' 40" (51o 50.6') for the North face weighted mean.
Hence Petrie=s weighted mean falls in the mid-range of the theoretical ideals, and almost exactly on the 11/14 ratio.
The ideal slopes for these three are:
#1 1.2732
#2 1.2720
#3 1.2728
Petrie=s measured slope is 1.274.
Petrie noted differences among the four sides of the pyramid. A concavity exists on each of the sides, and makes the exact determination of construction intent impossible.
Hence we shall never be able to conclude one way or the other which of these three criteria were used to design the Great Pyramid.
Putting Pieces Together
Petrie was aware of the integral Pythagorean triangles in the pyramids. He said that the use of ratios:
All four integral heights seem to be the starting point for calculating the base lengths. These are 200 cubits for the two pyramids at Daschur, 275 cubits for Giza 2, and 280 cubits for Giza 1.
Now a curious question raises itself. If Giza 2 were increased in height to that of its companion, 280 cubits from 275, as we see for the two pyramids at Daschur, the length of the base would increase from 410.8 to 421.2 cubits.
The base length of the Flat is 418.5 cubits.
These two values differ by only 3 cubits.
If we were to sketch the outlines of the four pyramids to scale for this idealized scheme we would discover that the two Giza pyramids would touch at the top, the two Daschur pyramids would touch at the top, the Bent falls within the outline of the Flat, and the Flat and Giza 2 very nearly coincide at the base.
Refer to the two sketches, one showing the designs as they were built, and the other according to this idealized scheme.
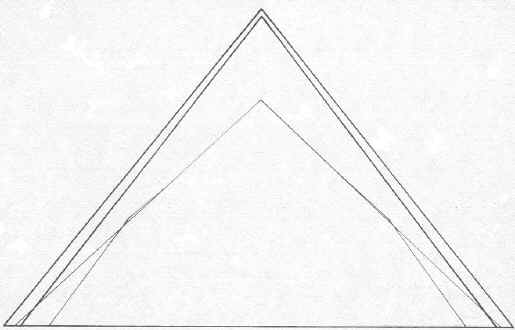 |
Outline of the Four Great Pyramids - As Built
Outline of the Four Great Pyramids - Ideal
Given the refinement of the great pyramid designs, and their clear connection to one another, why did the designer not make the Giza 2 height equal to Giza 1?
The cubit dimensions for Giza 2 of x, y, and a are 3/2 X 137, 4/2 X 137, and 5/2 X 137. 137 is a prime number. Prime numbers are used elsewhere in pyramid construction. Thus it is possible that the designer intended to make this display of mathematical knowledge, rather than simply equating the two Giza pyramid heights.
Such design ratios are in the other pyramids.
The Flat uses multiple of 10 to obtain the cubit measures: 20 X 10 for the height y, 21 X 10 for the base x, and 29 X 10 for the apothem, a.
If the Great Pyramid was designed according to the Archimedes ratio it uses multiples of 20 to obtain the cubit measures: 14 X 20 for the height y and 11 X 20 for the base x. The ratio of 14/11 does not provide an integral Pythagorean solution for the apothem, a.
Note that Giza 2 with a height of 280 cubits would have had multiples of 70 to obtain 3, 4, and 5 X 70, instead of multiples of a prime number.
The Bent pyramid uses multiples of 40/3 and 20/3 to obtain the simple trigonometric ratios.
The ratio of the height of the frustum to the base of the frustum is 93 1/3 to 66 2/3, or 7/5. The multiplication fact to obtain the cubit lengths is 40/3. Stated otherwise:
(93 1/3)/7 = (66 2/3)/5 = 40/3
The top of the Bent has a multiplication factor of 20/3:
(106 2/3)/16 = (113 1/3)/17 = 20/3.
The ratio of the two multiplication factors is 2:1.
These factors become more interesting when it is recognized that the frustum of the Bent contains numbers related to Giza 1 and the Flat.
The height of the frustum is 93 1/3 = 280/3 cubits. The width of the frustum is 66 2/3 = 200/3 cubits. Therefore the height of the Bent frustum is exactly 1/3 of the height of Giza 1, while the base of the frustum is exactly 1/3 the height of the Flat.
Or, to put it another way, the ratio of the height of Giza 1 to the height of the Flat is 7/5, and this is the slope of the Bent frustum.
Other factors should be noted:
Decimal multiples are used in Giza 1 (20) and the Flat (10). One is at Giza; one is at Daschur.
Fractional multiples (1/3) are used in the Bent. A primary number is used in Giza 2. One is at Giza; one is at Daschur.
Giza 2 and the Flat use integral Pythagorean relationships, 3-4-5 and 2B21-29. One is at Giza; one is at Daschur.
Giza 1 and the Bent do not use integral Pythagorean relationships. One is at Giza; one is at Daschur.
The decimal multiples and the integral Pythagorean numbers are not in the same structures at Giza and Daschur.
These design elements can be seen more clearly in the following table:
| Design Multiples | |||
| Decimal | Fractional | ||
| Relationships | Integral | Flat | Giza 2 |
| Non-integral | Giza 1 | Bent | |
This arrangement of elements can hardly be accidental, and shows intent by the designer to tie all four pyramids together in one grand architectural scheme.
The silliness of previous speculations can be noted from this remark by I. E. S. Edwards, who once held a wide reputation for his knowledge of the pyramids: